La volatilité implicite : guide complet

La volatilité implicite est un peu la météo des marchés financiers !

Et cet article est votre guide pour naviguer plus sereinement dans le climat changeant de la finance.

Imaginez-vous en tant que marin naviguant sur les mers tumultueuses des marchés financiers. Eh bien la volatilité implicite serait

Comme un météorologue prévoit les conditions climatiques, un bon investisseur en bourse sait interpréter la volatilité implicite pour être moins surpris par les mouvements du marché.

Vous allez voir que comprendre la volatilité implicite est une compétence essentielle pour les traders d’options que nous sommes vous et moi.

En la maîtrisant, vous saurez même vous méfier des marchés trop calmes, ou sortir les voiles quand les autres sont pris au dépourvu.

Suivez-nous pour comprendre les principes essentiels de la volatilité implicite !

Qu’est-ce que la Volatilité ?

Définition de la volatilité en finance.

La volatilité décrit le degré de variation des séries de rendements d’un titre ou d’un indice de marché. Plus précisément, elle mesure l’écart type ou la dispersion des rendements, fournissant ainsi une estimation du risque ou de l’incertitude associé à un investissement spécifique.

En termes plus simples, la volatilité, c’est comme des montagnes russes.

C’est une mesure qui nous dit à quel point le prix d’une action ou d’un indice de marché (comme le CAC 40 ou le Dow Jones) peut monter et descendre. Si les prix varient beaucoup, la volatilité est élevée ; s’ils restent plus ou moins constants, la volatilité est faible.

Cette variation des prix nous donne une idée du risque lié à un investissement. En gros, plus il y a de volatilité, plus le risque est grand !

Distinction entre volatilité historique et volatilité implicite.

Attention à ne pas confondre ces deux types principaux de volatilité : la volatilité historique et la volatilité implicite !

La volatilité historique, également connue sous le nom de volatilité réalisée ou statistique, est une mesure statistique utilisée en finance pour évaluer la variabilité ou la fluctuation des prix d’un actif financier au fil du temps.

Elle est souvent utilisée pour mesurer le risque associé à cet actif. La volatilité historique est calculée en analysant les variations passées des prix sur une période spécifique.

L’idée sous-jacente est que si un actif a connu de fortes variations de prix dans le passé, il est plus probable qu’il continue à fluctuer de manière similaire à l’avenir.

La volatilité historique est généralement mesurée en calculant l’écart-type des rendements d’un actif financier sur une période donnée. Les rendements représentent les variations de prix d’un actif, exprimées en pourcentage. L’écart-type est une mesure statistique qui permet de quantifier l’étendue des écarts par rapport à la moyenne.

Cette volatilité historique est utile pour plusieurs raisons.

Elle permet aux investisseurs d’évaluer le niveau de risque associé à un actif financier donné. Par exemple, si un actif a une volatilité historique élevée, on suppose qu’il peut continuer à subir des mouvements de prix brusques à l’avenir. Alors qu’un actif avec une volatilité historique faible peut être considéré comme plus stable et moins risqué.

Mais attention avec la volatilité historique ! Elle ne prévoit pas l’avenir avec certitude ! Les conditions de marché peuvent changer et les rendements passés ne garantissent pas les rendements futurs…

Cependant, cette volatilité historique donne une idée de la manière dont un actif a réagi aux événements passés. Cette information peut servir d’indice supplémentaire pour envisager les mouvements de prix futurs..

La volatilité implicite est différente. Elle mesure les fluctuations anticipées du prix d’un actif. Ces anticipations sont reflétées par le prix des options sur cet actif. Contrairement à la volatilité historique, la volatilité ne se base donc pas sur les données passées. Elle utilise la valeur des options en temps réel. Ce sont des données du présent cette fois-ci ! On dit de cette volatilité qu’elle est “implicite” dans le sens où elle n’est pas directement observable mais doit être déduite à partir du prix actuel d’une option. La volatilité implicite est cruciale pour la tarification des options. Elle est utilisée comme indicateur du sentiment des investisseurs à l’égard des fluctuations futures des prix.

Dans la pratique, il est souvent utile de considérer à la fois la volatilité historique et la volatilité implicite pour obtenir une perspective plus complète. La volatilité historique peut donner un aperçu des fluctuations passées et des schémas de comportement d’un actif, tandis que la volatilité implicite peut fournir des informations sur les attentes bien actuelles du marché. Attention cependant, il faut les interpréter avec prudence et ne les considérer que comme des outils d’évaluation du risque plutôt que comme des sources de prédiction infaillibles. Et il faut bien avoir en tête que ces deux volatilités sont indépendantes l’une de l’autre. Une volatilité historique élevée ne garantit absolument pas une volatilité implicite explosive. Et inversement, une volatilité historique au point mort n’est pas une preuve que la volatilité implicite va rester calme !

Ci-dessous, vous avez la volatilité historique du S&P 500 (20 jours) en bleu, et la volatilité implicite des options à 30 jours sur le S&P 500 en rouge (les 2 ne coïncident pas forcément) :

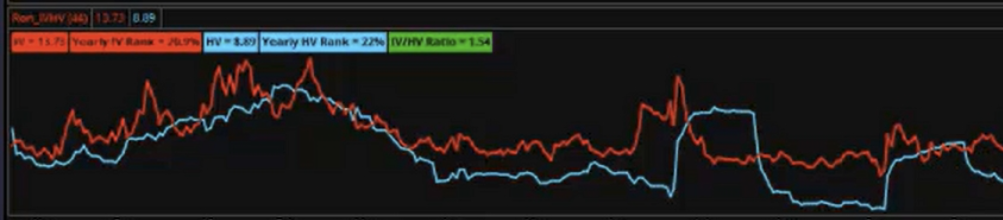
Comme vous le savez, les marchés financiers peuvent toujours réserver des surprises. Un actif ayant une volatilité historique et une volatilité implicite maximales peut tout à fait entrer en hibernation et s’arrêter soudainement de fluctuer ! Et inversement, le prix d’un actif qui “comate” depuis des années, et dont la volatilité implicite est minime, peut tout à fait s’énerver du jour au lendemain en explosant à la hausse, ou en s’écroulant !

La Volatilité Implicite Expliquée

Définition précise de la volatilité implicite.

La volatilité implicite est donc un concept essentiel dans le monde de la finance, et particulièrement pour nous, traders d’options.

Elle mesure la probabilité attendue d’un changement futur du prix d’un actif financier. Elle est calculée sur les prix actuels des options. Cette volatilité implicite est souvent exprimée en pourcentage de changements de prix anticipés sur une période d’un an.

Dans un sens, la volatilité implicite reflète les attentes des investisseurs quant à la volatilité future de l’actif sous-jacent. Une volatilité implicite élevée suggère que les investisseurs s’attendent à de grands mouvements de prix à l’avenir, tandis qu’une volatilité implicite faible indique que les investisseurs anticipent de faibles fluctuations de prix.

Voyons par l’exemple comment s’exprime la volatilité implicite :

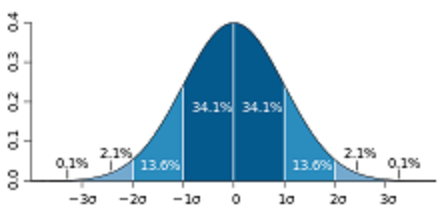
Considérons une action qui vaut 100$. Elle a une volatilité implicite de 20%. Cela signifie que son prix restera très probablement entre 80$ et 120$ au cours de l’année à venir. Cette variation de 20$ au-dessus et en dessous du prix actuel s’appelle un écart type. Cependant le cours de cette action peut aussi varier de deux écarts types, voire de trois écarts types ! Trois écarts type constituent une fourchette de prix allant de 40$ à 160$ (3x20=60 donc 60$ de variation). Mais pour chaque écart type supplémentaire, les probabilités diminuent un peu plus.

Si vous achetez une option d’achat d’actions pour laquelle il reste 30 jours avant l’échéance, cette volatilité implicite annuelle ne vous donne pas les informations dont vous avez besoin. Pour adapter cette volatilité implicite à la période de validité de votre option, vous devez faire un calcul. Il reste donc 30 jours avant la date d’échéance de notre option. Or il y a 12,17 périodes de 30 jours dans une année (365/30=12,17).

Vous devez donc diviser la volatilité implicite annuelle par la racine carrée de 12,17 (qui est de 3,49) : 20% / 3,49 = 5,7%.

Cela signifie que le mouvement attendu pour l’action sous-jacente au cours des 30 prochains jours est de 5,7% de son prix de 100$, soit 5,70$. Donc, elle se négocierait avec une probabilité de 68,2% entre 94,30$ et 105,70$ pendant cette période.

Rappelez-vous, ces chiffres correspondent à un seul écart type. Le prix pourrait bouger bien plus que cela (deux, trois écarts types, ou plus !).

Comment est calculée la volatilité implicite ?

La volatilité implicite est généralement calculée en utilisant des modèles de tarification d’options tels que le modèle Black-Scholes.

Ces modèles prennent en compte des facteurs tels que le prix actuel de l’actif sous-jacent, le prix d’exercice de l’option, le temps restant jusqu’à l’expiration de l’option, et le taux d’intérêt sans risque. Cependant, contrairement aux autres variables, la volatilité implicite n’est pas directement observable. Elle est plutôt déduite du prix actuel de l’option sur le marché. En pratique, on ajuste la volatilité dans le modèle de tarification jusqu’à ce que le prix de l’option calculé par le modèle corresponde au prix réel de l’option observé sur le marché.

Pourquoi la volatilité implicite est importante et comment est-elle utilisée par les investisseurs ?

La volatilité implicite joue un rôle crucial dans le monde de la finance pour plusieurs raisons.

Premièrement, elle est utilisée pour évaluer le coût relatif des options. Chaque option a son propre niveau de volatilité implicite et des options avec une volatilité implicite plus élevée seront généralement plus coûteuses, car elles sont associées à un risque plus élevé.

Deuxièmement, la volatilité implicite sert d’indicateur de l’incertitude ou du risque du marché. Par exemple, lors de périodes de grande incertitude, comme lors de la publication d’un rapport sur les résultats financiers d’une entreprise ou lors d’événements politiques majeurs, la volatilité implicite des options sur les actions concernées peut augmenter.

Enfin, la volatilité implicite est utilisée par les traders pour identifier les opportunités de trading. Par exemple, si un trader estime que la volatilité implicite d’une option est trop élevée par rapport à sa propre estimation de la volatilité future, il peut vendre l’option et réaliser un profit si la volatilité implicite diminue. À l’inverse, si un trader estime que la volatilité implicite est trop basse, il peut acheter l’option et réaliser un profit si la volatilité implicite augmente. C’est pour cela qu’on dit que lorsqu’on achète une option, on “achète de la volatilité”, et lorsqu’on vend une option, on “vend de la volatilité”.

Comprendre le Modèle Black-Scholes.

Introduction au modèle fondamental de Black-Scholes pour le calcul de la volatilité implicite.

Le modèle Black-Scholes, également appelé modèle Black-Scholes-Merton, est une approche mathématique développée par les économistes Fischer Black, Myron Scholes et Robert Merton, pour évaluer le prix des options financières. Publié pour la première fois en 1973, ce modèle est devenu un outil essentiel pour les traders et les analystes financiers, notamment pour le calcul de la volatilité implicite.

Explication des composants du modèle et de son fonctionnement.

Le modèle Black-Scholes est basé sur un certain nombre de suppositions, et utilise ces suppositions pour dériver une équation différentielle partielle qui est ensuite résolue pour obtenir le prix d’une option.

Les composants clés de ce modèle comprennent :

1. Le prix actuel de l’actif sous-jacent
2. Le prix d’exercice de l’option
3. Le temps restant jusqu’à l’expiration de l’option
4. Le taux d’intérêt sans risque
5. La volatilité du prix de l’actif sous-jacent

Les limites du modèle, et comment il peut être ajusté.

Bien que le modèle Black-Scholes soit largement utilisé, il comporte des limitations importantes.

Parmi celles-ci figurent les suppositions que la volatilité et le taux d’intérêt sont constants, que les rendements sont normalement distribués et que le marché est parfait (pas de frais de transaction, possibilité d’emprunter et de prêter au taux d’intérêt sans risque, etc.). En réalité, ces suppositions ne tiennent souvent pas.

En particulier l’hypothèse que la volatilité des options sur un sous-jacent est la même quelque soit la date d’échéance et le prix d’exercice n’est pas juste, vous trouverez plus d’informations à ce sujet dans

Afin de surmonter certaines de ces limitations, des variations du modèle Black-Scholes ont été développées. Par exemple, le modèle Black-Scholes peut être étendu pour prendre en compte les dividendes versés par l’actif sous-jacent. De plus, des modèles plus sophistiqués tels que le modèle Heston ou le modèle SABR permettent de prendre en compte une volatilité qui varie dans le temps.

Malgré ses limites, le modèle Black-Scholes reste un outil fondamental dans le domaine de la finance, et sa compréhension est essentielle pour quiconque souhaite travailler avec des options ou d’autres produits dérivés.

Autres Modèles de pricing des options.

Bien que le modèle Black-Scholes soit le plus célèbre et le plus couramment utilisé, il existe d’autres modèles pour déterminer le prix des options qui méritent d’être mentionnés. Certains de ces modèles tentent de surmonter les limites du modèle Black-Scholes et de fournir une représentation plus précise du monde réel.

Modèle de Heston.

Le modèle de Heston est un modèle de prix d’option qui a été développé par Steven Heston en 1993. C’est un modèle de volatilité stochastique, ce qui signifie qu’il prend en compte le fait que la volatilité d’un actif financier peut changer au fil du temps et n’est pas constante. Le modèle de Heston est particulièrement utile pour la tarification des options car il permet de prendre en compte la “volatilité de la volatilité” - la mesure dans laquelle la volatilité elle-même est volatile. L’une des principales caractéristiques du modèle de Heston est qu’il permet d’obtenir un “smile de volatilité”, où la volatilité implicite d’une option peut varier en fonction de son prix d’exercice. C’est quelque chose que le modèle Black-Scholes ne peut pas faire, car il suppose que la volatilité est constante.

Modèle SABR.

Le modèle SABR (Stochastic Alpha, Beta, Rho) est un autre modèle de volatilité stochastique qui a été développé par Hagan et al. en 2002. Ce modèle est souvent utilisé pour la tarification des dérivés d’intérêts, tels que les swaptions ou les caplets. Le modèle SABR a quatre paramètres : l’alpha, qui représente la volatilité de l’actif ; le bêta, qui contrôle la skewness (asymétrie) de la distribution des rendements de l’actif ; le rho, qui est la corrélation entre les mouvements de l’actif et sa volatilité ; et le nu, qui est la volatilité de la volatilité. L’un des avantages du modèle SABR est qu’il est capable de reproduire le smile de volatilité observé dans les marchés d’options.

Il est important de noter que ces deux derniers modèles sont plus complexes que le modèle Black-Scholes et nécessitent plus de calculs. Cependant, ils peuvent offrir une meilleure estimation du prix des options, en particulier pour les options exotiques ou dans les marchés où la volatilité est importante.

Modèle Binomial.

Le modèle binomial est un autre modèle très couramment utilisé pour évaluer les options. Il fonctionne en créant un arbre binomial qui représente les mouvements possibles du prix de l’actif sous-jacent sur une période de temps. Le principal avantage du modèle binomial est sa flexibilité. Il peut être utilisé pour évaluer des options de type américain, qui peuvent être exercées à tout moment jusqu’à l’échéance, contrairement aux options de type européennes, qui ne peuvent être exercées qu’à l’échéance.

Imaginez que vous jouez à un jeu de pile ou face. À chaque fois que vous lancez la pièce, vous pouvez obtenir pile ou face. Le modèle binomial est un peu comme ça. Il crée un arbre de décisions où, à chaque étape, le prix de l’option peut augmenter ou diminuer. Ce qui est bien avec le modèle binomial, c’est qu’il est très flexible. C’est grâce à cette qualité qu’il peut être utilisé pour les options de type américain.

Modèle trinomial.

Le modèle trinomial est une extension du modèle binomial. Il ajoute une troisième branche à l’arbre de prix, ce qui permet au prix de l’actif sous-jacent de rester inchangé au cours d’une période de temps, en plus de pouvoir monter ou descendre. Le modèle trinomial est plus précis que le modèle binomial, mais il est également plus complexe et nécessite plus de calculs.

Le modèle trinomial est une version améliorée du modèle binomial. Au lieu de deux choix (comme pile ou face), vous avez donc maintenant trois choix. Le prix de l’option peut augmenter, diminuer, ou rester le même. C’est comme si vous lanciez un dé à trois faces au lieu d’une pièce à deux faces.

Modèle Bachelier.

Le modèle Bachelier, également connu sous le nom de modèle de distribution normale, est un autre modèle qui diffère du modèle Black-Scholes en ce qu’il suppose que les rendements de l’actif sous-jacent sont normalement distribués, plutôt que log-normalement distribués comme dans le modèle Black-Scholes. Cette hypothèse peut rendre le modèle Bachelier plus approprié pour certaines options, telles que les options sur taux d’intérêt.

Expliquons cela en termes plus accessibles. Au lieu de supposer que le prix de l’option change comme dans une course de chevaux (avec des gagnants clairs et des perdants clairs), il suppose que le prix de l’option change plus comme la taille des personnes dans une population : la plupart des gens sont de taille moyenne, mais certains sont plus grands ou plus petits. C’est ce qu’on appelle une “distribution normale”.

Notez bien que même si ces modèles peuvent être plus adaptés à certaines situations, aucun modèle de tarification des options n’est parfait. Chaque modèle repose sur des hypothèses qui simplifient la réalité. Par conséquent, les investisseurs doivent comprendre les hypothèses et les limitations de chaque modèle lorsqu’ils les utilisent pour évaluer les options.

La Volatilité Implicite et les Options.

Le lien entre la volatilité implicite et les options.

La volatilité implicite a un lien étroit et crucial avec les options. Pour faire simple, la volatilité implicite est une mesure du mouvement anticipé de l’actif sous-jacent d’une option. Ainsi, la volatilité du prix de cet actif est d’une grande importance pour la valorisation de l’option.

Comment la volatilité implicite influence le prix des options ?

Le prix des options est influencé par plusieurs facteurs, dont la volatilité implicite est l’un des plus importants. En fait, tout autre facteur étant égal par ailleurs, une augmentation de la volatilité implicite entraînera une augmentation du prix des options, qu’elles soient d’achat (call) ou de vente (put).

Cela est dû au fait que lorsque la volatilité augmente, le potentiel de mouvement du prix de l’actif sous-jacent est plus grand, augmentant ainsi la probabilité que l’option finisse dans la monnaie. Par conséquent, une option dans un environnement de forte volatilité sera plus chère qu’une option similaire dans un environnement de faible volatilité.

L’effet de la volatilité implicite sur différentes stratégies d’options.

La volatilité implicite a une influence majeure sur la prime des options. Il est fondamental de la prendre en compte lors de la mise en place de vos stratégies sur options.

En effet, une hausse brutale de la volatilité implicite augmente fortement la valeur d’une option. Cette situation est favorable aux acheteurs d’options, mais elle est dangereuse pour les vendeurs d’options. A l’inverse, une baisse soudaine de cette volatilité implicite implique un gain latent pour le vendeur d’option, et une perte latente pour l’acheteur.

Le tableau ci-dessous expose de manière explicite l’énorme influence de la volatilité implicite sur le cours des options. Vous pouvez constater que lorsque la volatilité implicite passe de 30% à 100% toutes autres conditions égales par ailleurs, la prime de l’option augmente de plus de 200% !

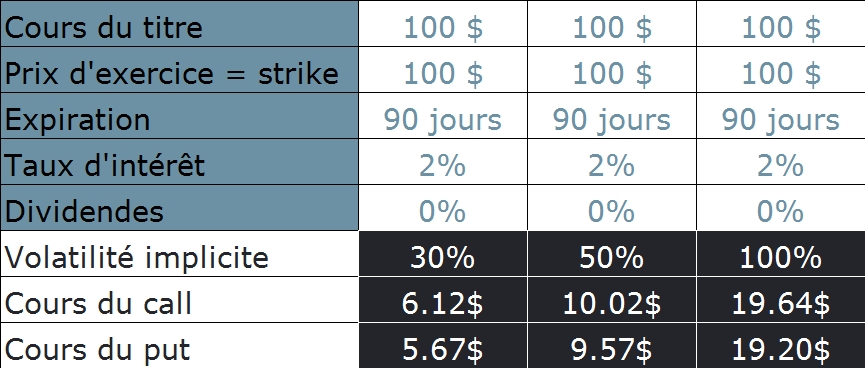
L’influence de la volatilité implicite sur un montage d’options (impliquant plus qu’une seule option) est plus complexe. Nous vous recommandons fortement d’utiliser un outil simulateur pour vous préparer à toutes les situations possibles en matière de volatilité implicite et ne pas vous faire surprendre.

Présentation du concept de “smile de volatilité”.

Le “smile de volatilité” est un concept qui a émergé après le krach boursier de 1987 et qui décrit une particularité observée dans la structure de la volatilité implicite des options.

Lorsqu’on trace la volatilité implicite en fonction du prix d’exercice de l’option, plutôt que d’obtenir une ligne droite comme le supposerait le modèle Black-Scholes, on observe généralement une courbe en forme de sourire. Cette courbe indique que la volatilité implicite est généralement plus élevée pour les options en dehors de la monnaie (out of the money) et dans la monnaie (in the money), et plus faible pour les options à la monnaie (at the money).

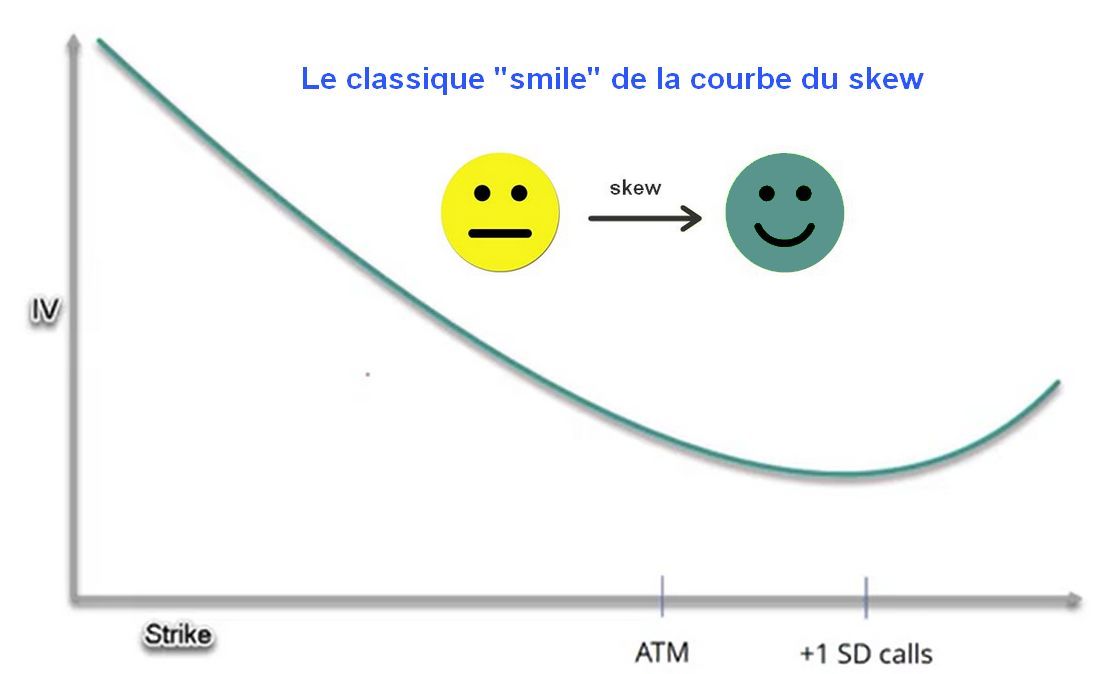
Le smile de volatilité montre que le marché attribue une probabilité plus élevée à de grands mouvements de prix (à la hausse ou à la baisse) qu’au modèle Black-Scholes. Il peut être causé par plusieurs facteurs, tels que la demande et l’offre sur le marché des options, la peur des événements de queue (grands mouvements de prix imprévus) et les imperfections du modèle Black-Scholes. Pour en savoir plus, allez consulter notre article consacré au skew en cliquant ici.

La Volatilité Implicite et le Risque.

Comment la volatilité implicite peut être utilisée comme indicateur du risque.

La volatilité implicite est considérée comme un indicateur de risque dans le domaine financier. En règle générale, une volatilité implicite élevée est associée à un degré de risque plus élevé. La raison en est simple : une volatilité élevée indique que les acteurs du marché anticipent de grands mouvements de prix à venir pour l’actif sous-jacent.

En effet, les acheteurs d’options sont prêts à payer plus cher la garantie offerte par un put ou un call. Et de l’autre côté, les vendeurs d’options exigent un prix plus élevé pour supporter la charge de cette garantie. Cela peut être le résultat de l’incertitude entourant les futures performances de l’actif ou de l’économie en général.

Par conséquent, un trader peut utiliser la volatilité implicite comme un indicateur pour évaluer le niveau de risque associé à un investissement particulier. Par exemple, une option avec une volatilité implicite élevée peut signifier un risque plus élevé, mais également une opportunité de rendements plus élevés. En revanche, une option avec une faible volatilité implicite peut présenter un risque moindre, mais aussi des rendements potentiels moins élevés.

Il ne faut cependant pas chercher de certitudes, y compris avec la volatilité implicite. Car un actif ayant une très forte volatilité implicite peut finalement rester très calme, et un autre actif à faible volatilité implicite peut exploser dans un sens ou dans l’autre.

Explication de la notion de “volatilité implicite anticipée”.

La notion de “volatilité implicite anticipée” se réfère à une estimation future de la volatilité implicite.

La volatilité implicite est une mesure qui est constamment mise à jour et change en fonction des conditions du marché. Car à tout moment les intervenants essaient d’anticiper la direction dans laquelle la volatilité implicite se déplacera.

Autrement dit, ils tentent de prévoir comment l’incertitude du marché évoluera. Les traders peuvent utiliser une variété d’outils et de techniques pour tenter de prévoir cette volatilité implicite future. Ces outils incluent les modèles statistiques, l’analyse des nouvelles et des événements économiques, ainsi que le sentiment du marché. Toutefois, comme toute forme de prévision, l’anticipation de la volatilité implicite comporte un degré d’incertitude et de risque. Il faut rester prudent si l’on utilise la volatilité implicite dans une prise de décision.

Par exemple, si le prix d’un indice se met à baisser, et que cette baisse devient une chute qui s’accélère brutalement, il risque d’y avoir un effet de panique. Les investisseurs vont se précipiter sur les puts (options de vente) afin de protéger leurs portefeuilles. Au même moment, des spéculateurs vont également chercher à profiter d’un potentiel début de krack et ils vont également acheter des puts. Sous cette pression acheteuse, les prix des puts peuvent exploser à la hausse en quelques minutes ! En effet, sous l’effet de la panique, la volatilité implicite de l’indice explose car presque tout le monde s’attend à un krach boursier.

Cela fonctionne aussi dans l’autre sens, comme avec l’action GameStop en janvier 2020. A l’époque, une communauté de spéculateurs s’était organisée pour créer une pression acheteuse sur l’action, et mettre en difficulté les institutionnels qui shortaient le titre. Ceux-ci étaient sous pression, car toute hausse de l’action augmentait leurs pertes latentes. Comme on peut le voir sur le graphe ci-dessous, un sursaut haussier de l’action provoquait immédiatement une hausse exponentielle du prix d’un call hors de la monnaie. Du fait de la nervosité des intervenants, et de l’effet “short squeeze” (prix poussé à la hausse grâce aux clôtures de positions short), les intervenants s’attendaient à une explosion haussière à tout moment.

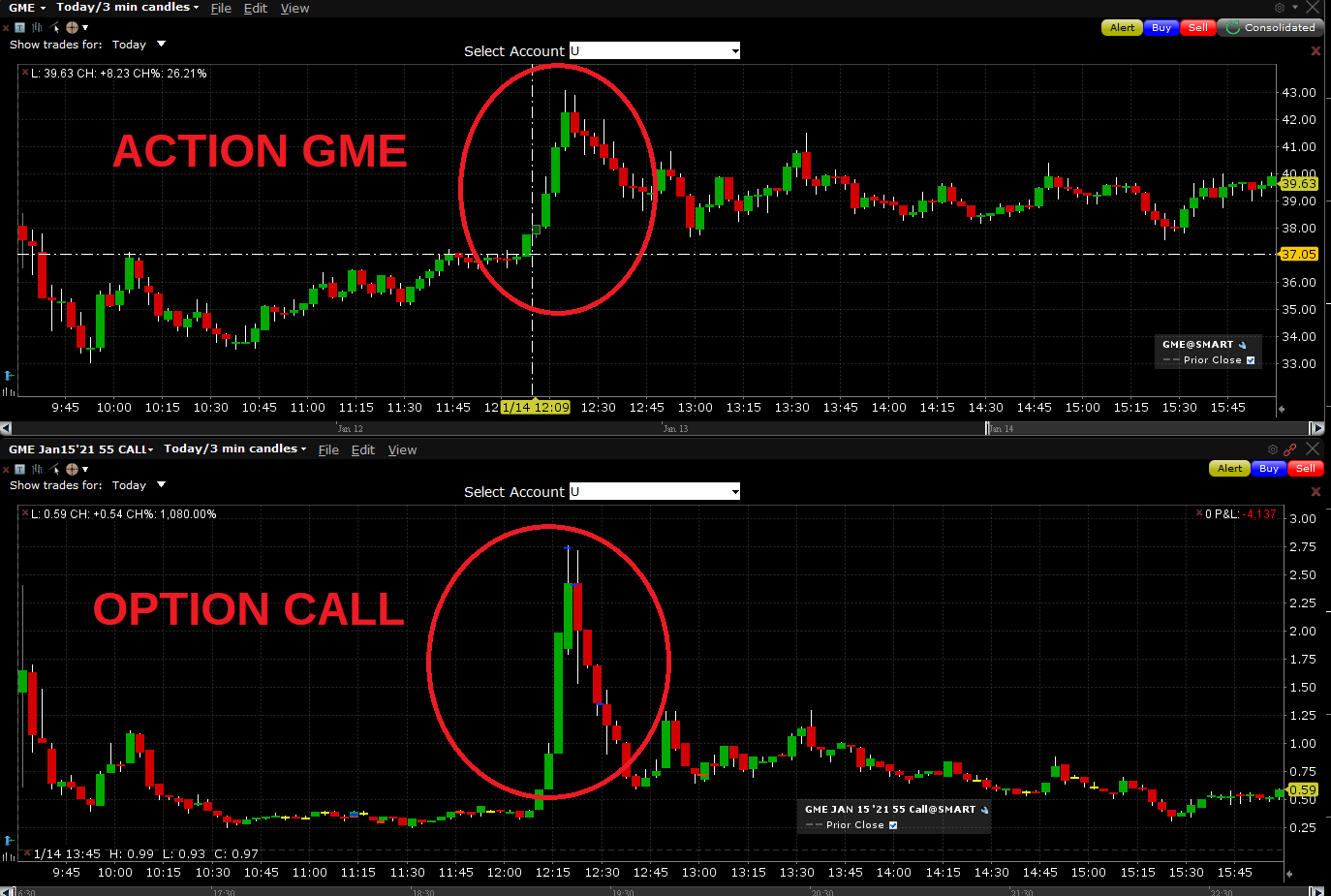
Les Indices de Volatilité.

Un aspect pratique de la volatilité implicite est l’utilisation des indices de volatilité. Ces indices, tels que le VIX (Volatility Index), fournissent une mesure de la volatilité du marché attendue par les participants au marché.

Le VIX, souvent appelé “l’indice de la peur”, est basé sur la volatilité implicite des options sur l’indice S&P 500. C’est un outil précieux pour les traders et les investisseurs car il donne une indication du sentiment du marché et de la volatilité attendue. Lorsque le VIX est élevé, cela signifie généralement que les investisseurs anticipent une volatilité accrue, ce qui est souvent associé à une plus grande incertitude ou à la peur. À l’inverse, un VIX bas peut indiquer une attente de stabilité sur le marché.

Il est important de noter que le VIX et d’autres indices de volatilité sont des outils d’analyse et ne prédisent pas directement les mouvements futurs du marché. Ils représentent plutôt le consensus du marché sur la volatilité future. Ainsi, en comprenant comment ces indices de volatilité fonctionnent et ce qu’ils représentent, vous pouvez améliorer votre capacité à évaluer le sentiment du marché, à identifier les opportunités d’investissement ou de trading d’options, et à gérer le risque dans votre portefeuille.

D’autres indices de volatilité sont le VXN (Nasdaq-100 Volatility Index), le VXD (Dow Jones Industrial Average Volatility Index), le RVX (Russell 2000 Volatility Index), l’EVZ (Euro Stoxx 50 Volatility Index) et le VXFXI (FTSE China 50 Volatility Index).

La volatilité implicite et le marché global.

La volatilité implicite ne se crée pas à partir de rien ! Elle est influencée par une multitude de facteurs sur le marché global, comme les événements macroéconomiques tels que les changements de taux d’intérêt, les données de l’emploi, les guerres commerciales, et les crises politiques.

Un changement inattendu de taux d’intérêt, par exemple, peut avoir un impact significatif sur la volatilité implicite. Un relèvement des taux d’intérêt peut entraîner une augmentation de la volatilité implicite car il augmente le coût du capital, ce qui peut réduire les investissements et ralentir la croissance économique. Inversement, une réduction des taux d’intérêt peut réduire la volatilité implicite en rendant le capital moins cher, ce qui peut stimuler les investissements et la croissance économique.

Il est utile de suivre les événements macroéconomiques et de comprendre comment ils peuvent affecter la volatilité implicite. Il est ainsi plus facile d’évaluer le risque associé à un investissement et de prendre des décisions éclairées.

Il est également important de noter que la volatilité implicite est souvent considérée comme un indicateur avancé des mouvements du marché. Une volatilité implicite en hausse peut indiquer une incertitude croissante sur le marché et peut souvent précéder une baisse des prix des actions.

À l’inverse, une volatilité implicite en baisse peut signaler une confiance accrue des investisseurs et peut souvent coïncider avec une hausse des prix des actions. Il ne faut cependant pas prendre ces principes à la lettre. Car une volatilité peut être à son maximum juste à la fin d’un krach. Elle peut également être à un niveau minimum quelques minutes avant une chute brutale. C’est le calme avant la tempête en quelque sorte.

Comment Utiliser la Volatilité Implicite dans vos Investissements.

Utiliser la volatilité implicite dans vos décisions d’investissement.

Voici quelques conseils pratiques pour éclairer vos décisions d’investissement avec la volatilité implicite.

• Évaluation du risque : Utilisez la volatilité implicite pour estimer le niveau de risque associé à une option particulière ou à un autre produit dérivé. Une volatilité implicite élevée pourrait indiquer un risque plus grand, mais aussi un potentiel de rendement plus élevé.
• Comparaison des options : Comparez la volatilité implicite de différentes options pour identifier celles qui peuvent offrir le meilleur équilibre entre le risque et le rendement.
• Analyse du marché : Utilisez la volatilité implicite comme un baromètre pour comprendre le sentiment général du marché. Une volatilité implicite élevée peut indiquer une incertitude accrue sur le marché.

Comparaison de la volatilité implicite entre différents actifs et marchés.

Il est important pour tout investisseur de comprendre que la volatilité implicite peut varier considérablement d’un actif à l’autre, et d’un marché à l’autre. Cette variabilité reflète les différences de perception du risque par les participants au marché.

Par exemple, la volatilité implicite d’une option sur une action individuelle peut être significativement différente de celle d’une option sur un ETF d’indice boursier. Cela est dû à des facteurs tels que les perspectives de l’entreprise, le secteur d’activité, la santé financière de l’entreprise et d’autres facteurs spécifiques à l’entreprise qui peuvent influencer la volatilité de son cours de bourse. Par ailleurs, une option sur un ETF d’indice boursier, qui regroupe de nombreuses actions, a tendance à avoir une volatilité implicite plus faible, car les mouvements individuels des actions se compensent en partie.

De même, la volatilité implicite peut varier d’un marché à l’autre. Par exemple, les options sur les marchés de matières premières peuvent avoir une volatilité implicite plus élevée en raison de l’incertitude liée aux conditions météorologiques, aux conflits politiques, aux modifications de la politique monétaire et à d’autres facteurs macroéconomiques.

La compréhension de ces variations de la volatilité implicite entre différents actifs et marchés peut aider les investisseurs à construire un portefeuille diversifié. La volatilité implicite peut aussi leur permettre de comprendre où se trouvent les risques et les opportunités, et à ajuster leur stratégie d’investissement en conséquence.

Exemples de stratégies d’investissement basées sur la volatilité implicite.

Voici quelques stratégies d’investissement que vous pouvez explorer qui exploitent la volatilité implicite:

• Stratégies de vente d’options : Lorsque la volatilité implicite est élevée, les options ont tendance à être plus chères. Les vendeurs d’options peuvent profiter de cette situation en vendant des options lorsque la volatilité est élevée, puis en les rachetant lorsque la volatilité diminue.
• Stratégies d’achat d’options : Inversement, lorsque la volatilité implicite est faible, les options ont tendance à être moins chères. Les acheteurs d’options peuvent profiter de cette situation en achetant des options lorsque la volatilité est faible, puis en les vendant lorsque la volatilité augmente.
• Stratégies de volatilité : Certaines stratégies visent spécifiquement à tirer profit des changements de volatilité, indépendamment de la direction du prix de l’actif sous-jacent. Par exemple, un “long straddle” est une stratégie qui implique l’achat d’une option d’achat et d’une option de vente avec le même prix d’exercice et la même date d’expiration. Si la volatilité augmente suffisamment, la stratégie peut devenir rentable, indépendamment de la direction dans laquelle le prix de l’actif évolue.

Ces stratégies ne sont que quelques exemples de la façon dont la volatilité implicite peut orienter vos choix de stratégies sur options. Il est cependant indispensable de se former afin de bien comprendre ce que vous faites.

Conclusion

Félicitations ! En apprenant le concept de volatilité implicite, vous avez passé une étape importante de votre apprentissage des options ! Vous avez mieux compris comment une option est valorisée, et vous disposez d’un indicateur supplémentaire pour vos prises de décision en bourse ! Si tout n’est pas encore parfaitement clair, ne vous inquiétez pas, avec la pratique, vous allez assimiler de mieux en mieux cette notion indispensable aux acheteurs et vendeurs d’options. Pour cela, vous pouvez vous laisser guider par nos formations sur options (lien vers pack) puis commencer à pratiquer chez l’un de nos deux courtiers préférés :